Integral indefinida
Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de f de x diferencial de x.
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.
Propiedades de la integral indefinida
1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
∫ k f(x) dx = k ∫f(x) dx
INTEGRALES INDEFINIDAS
Usted está familiarizado con algunas operaciones inversas. La adición y la sustracción son operaciones inversas, la multiplicación y la división son también operaciones inversas, así como la potenciación y la extracción de raíces. Ahora, conocerá la operación inversa la de derivación o diferenciación denominada antiderivación o antidiferenciación, la cual implica el cálculo de una antiderivada.
Antiderivada.
Una función F se denomina antiderivada de una función f en un intervalo I si  para todo
para todo 
 para todo
para todo 
Ejemplo.
Si F es la función definida por  entonces
entonces  De modo que si
De modo que si  entonces f es la derivada de F, y F es la antiderivada de f. Si G es la función definida por
entonces f es la derivada de F, y F es la antiderivada de f. Si G es la función definida por  entonces G también es una antiderivada de f, porque
entonces G también es una antiderivada de f, porque  En realidad, cualquier función H definida por
En realidad, cualquier función H definida por  donde C es una constante, es una antiderivada de f.
donde C es una constante, es una antiderivada de f.
 entonces
entonces  De modo que si
De modo que si  entonces f es la derivada de F, y F es la antiderivada de f. Si G es la función definida por
entonces f es la derivada de F, y F es la antiderivada de f. Si G es la función definida por  entonces G también es una antiderivada de f, porque
entonces G también es una antiderivada de f, porque  En realidad, cualquier función H definida por
En realidad, cualquier función H definida por  donde C es una constante, es una antiderivada de f.
donde C es una constante, es una antiderivada de f.
Teorema 1.
Si f y g son dos funciones definidas en el intervalo I, tales que  para todo
para todo  entonces existe una constante K tal que
entonces existe una constante K tal que  para todo
para todo 
 para todo
para todo  entonces existe una constante K tal que
entonces existe una constante K tal que  para todo
para todo 
"La antiderivación o antidiferenciación es el proceso mediante el cual se determina el conjunto de todas las antiderivadas de una función dada. El símbolo  denota la operación de antiderivación, y se escribe
denota la operación de antiderivación, y se escribe  donde
donde  y
y 
 denota la operación de antiderivación, y se escribe
denota la operación de antiderivación, y se escribe  donde
donde  y
y 
En la igualdad x es la variable de integración,
x es la variable de integración,  es el integrando y la expresión
es el integrando y la expresión  recibe el nombre de antiderivada general o integral indefinida de f. Si
recibe el nombre de antiderivada general o integral indefinida de f. Si  es el conjunto de todas las funciones cuyas diferenciales sean
es el conjunto de todas las funciones cuyas diferenciales sean  también es el conjunto de todas las funciones cuya derivada es
también es el conjunto de todas las funciones cuya derivada es 
 x es la variable de integración,
x es la variable de integración,  es el integrando y la expresión
es el integrando y la expresión  recibe el nombre de antiderivada general o integral indefinida de f. Si
recibe el nombre de antiderivada general o integral indefinida de f. Si  es el conjunto de todas las funciones cuyas diferenciales sean
es el conjunto de todas las funciones cuyas diferenciales sean  también es el conjunto de todas las funciones cuya derivada es
también es el conjunto de todas las funciones cuya derivada es 
Teorema 2.

Teorema 3.
 donde a es una constante.
donde a es una constante.
Teorema 4.
Si las funciones f y g están definidas en el mismo intervalo, entonces 

Teorema 5.
Si las funciones  están definidas en el mismo intervalo, entonces
están definidas en el mismo intervalo, entonces 
 están definidas en el mismo intervalo, entonces
están definidas en el mismo intervalo, entonces 
donde  son constantes.
son constantes.
 son constantes.
son constantes.
Teorema 6.
Si n es un número racional, entonces 

Ejemplos.
1) Evalúe 

Solución.

2) Calcule 

Solución.

3) Determine 

Solución.

Los teoremas para las integrales indefinidas de las funciones trigonométricas seno, coseno, secante al cuadrado, cosecante al cuadrado, secante por tangente y cosecante por cotangente, son deducciones inmediatas de los teoremas correspondientes de diferenciación. A continuación se presentan tales teoremas.
Teorema 7.
 Teorema 8.
Teorema 8.
Teorema 9.

Teorema 10.

Teorema 11.

Teorema 12.

Ejemplos.
1) Evalúe 

Solución.

Las identidades trigonométricas se emplean con frecuencia cuando se calculan integrales indefinidas que involucran funciones trigonométricas. Las ocho identidades trigonométricas fundamentales siguientes son de crucial importancia.

2) Calcule 

Solución.

3) Determine 

Solución.

Ejercicios.
Calcule las integrales indefinidas:
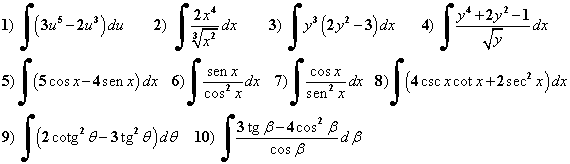
Teorema 13. Regla de la cadena para antiderivación.
Sea g una función diferenciable y sea el contradominio de g algún intervalo I. Suponga que f es una función definida en I y que F es una antiderivada de f en I. Entonces 

Teorema 14.
Si g es una función diferenciable y n es un número racional, entonces 

Ejemplos.
1) Evalúe 

Solución.

y observe que si  entonces
entonces  Por lo tanto, se necesita un factor 3 junto a
Por lo tanto, se necesita un factor 3 junto a  para obtener
para obtener  En consecuencia, se escribe
En consecuencia, se escribe
 entonces
entonces  Por lo tanto, se necesita un factor 3 junto a
Por lo tanto, se necesita un factor 3 junto a  para obtener
para obtener  En consecuencia, se escribe
En consecuencia, se escribe
2) Calcule 

Solución.
Observe que si  entonces
entonces  Por lo tanto, necesitamos un factor 6 junto a
Por lo tanto, necesitamos un factor 6 junto a  para obtener
para obtener  Luego, se escribe
Luego, se escribe 
 entonces
entonces  Por lo tanto, necesitamos un factor 6 junto a
Por lo tanto, necesitamos un factor 6 junto a  para obtener
para obtener  Luego, se escribe
Luego, se escribe 
- 3) Evalúe

Solución.
Como  se escribe
se escribe 
 se escribe
se escribe 
Ejercicios.
Resuelva:

En los teoremas que se presentan a continuación  es una función de x, es decir,
es una función de x, es decir, 
 es una función de x, es decir,
es una función de x, es decir, 
Teorema 15.

Ejemplo.
Evalúe 

Solución.
En este caso  por lo tanto,
por lo tanto,  luego se necesita un factor 3 junto a
luego se necesita un factor 3 junto a  para obtener
para obtener  Entonces, se escribe
Entonces, se escribe
 por lo tanto,
por lo tanto,  luego se necesita un factor 3 junto a
luego se necesita un factor 3 junto a  para obtener
para obtener  Entonces, se escribe
Entonces, se escribe
Teorema 16.

Ejemplo.
Calcule 

Solución.
Consideremos  tenemos que
tenemos que  luego necesitamos un factor 6 junto a
luego necesitamos un factor 6 junto a  para obtener
para obtener  Por lo tanto,
Por lo tanto,
 tenemos que
tenemos que  luego necesitamos un factor 6 junto a
luego necesitamos un factor 6 junto a  para obtener
para obtener  Por lo tanto,
Por lo tanto,
Teorema 17.

Ejemplo.
Calcule 

Solución.
Como  entonces
entonces  por lo tanto,
por lo tanto,
 entonces
entonces  por lo tanto,
por lo tanto,
Teorema 18.

Ejemplo.
Evalúe 

Solución.
Siendo  entonces
entonces  luego, podemos escribir
luego, podemos escribir
 entonces
entonces  luego, podemos escribir
luego, podemos escribir
Teorema 19.

Ejemplo.
Resuelva 

Solución.
Ejercicios.
Resuelva las integrales indefinidas:
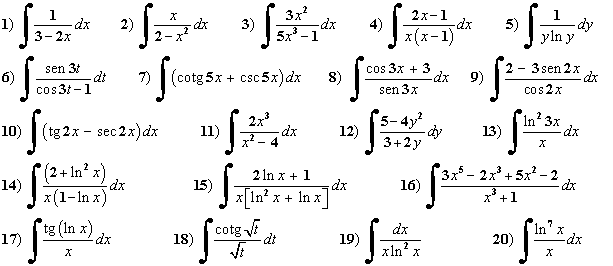
Teorema 20.

Ejemplo.
Evalúe 

Solución.
Sea  entonces,
entonces,  por lo tanto
por lo tanto
 entonces,
entonces,  por lo tanto
por lo tanto
Teorema 21.

Ejemplo.
Evalúe 

Solución.
Como  se aplica el teorema 21 con
se aplica el teorema 21 con  de donde obtenemos,
de donde obtenemos,  entonces
entonces
 se aplica el teorema 21 con
se aplica el teorema 21 con  de donde obtenemos,
de donde obtenemos,  entonces
entonces
Ejercicios.
En los siguientes ejercicios evalúe la integral indefinida.

A partir de las fórmulas de las derivadas de las funciones trigonométricas inversas se obtienen algunas fórmulas de integrales indefinidas. El teorema siguiente proporciona tres de estas fórmulas.
Teorema 22.


El teorema siguiente proporciona algunas fórmulas más generales.
Teorema 23.


Ejemplos.
1) Evalúe 

Solución.

2) Evalúe 

Solución.

Con la finalidad de completar el cuadrado de  se suma
se suma  y como está multiplicado por 3 en realidad se suma es
y como está multiplicado por 3 en realidad se suma es  al denominador, de modo que para que la expresión del denominador persista, es decir, no se altere, se resta también
al denominador, de modo que para que la expresión del denominador persista, es decir, no se altere, se resta también  Por lo tanto, se tiene
Por lo tanto, se tiene
 se suma
se suma  y como está multiplicado por 3 en realidad se suma es
y como está multiplicado por 3 en realidad se suma es  al denominador, de modo que para que la expresión del denominador persista, es decir, no se altere, se resta también
al denominador, de modo que para que la expresión del denominador persista, es decir, no se altere, se resta también  Por lo tanto, se tiene
Por lo tanto, se tiene
3) Evalúe 

Solución.


Las fórmulas de integración indefinida del teorema siguientes son consecuencia inmediata de las fórmulas de las derivadas de las funciones hiperbólicas.
Teorema 24.




Ejemplos.
1) Evalúe 

Solución.

2) Evalúe 

Ejercicios.

Antes de estudiar los diferentes métodos de integración, se presenta una lista numerada de las fórmulas típicas de integración indefinida las cuales deben ser memorizadas por el estudiante para un mejor desenvolvimiento.


Emprendamos el estudio de los métodos de integración. Uno de los métodos más ampliamente usados en la resolución de integrales es la integración por partes.
INTEGRACIÓN POR PARTES
La fórmula de la integración por partes es la siguiente:

Esta fórmula expresa a la integral  en términos de la integral
en términos de la integral  Mediante una elección adecuada de u y dv, puede evaluarse más fácilmente integral
Mediante una elección adecuada de u y dv, puede evaluarse más fácilmente integral 
 en términos de la integral
en términos de la integral  Mediante una elección adecuada de u y dv, puede evaluarse más fácilmente integral
Mediante una elección adecuada de u y dv, puede evaluarse más fácilmente integral 
Ejemplos.
1) Evaluar 

Solución.
Tomemos u = ln x y dv = x dx, por lo tanto,  y
y  luego,
luego, 
 y
y  luego,
luego, 
2) Evaluar 

Solución.

Sea  y
y  entonces,
entonces,  y
y  por lo tanto,
por lo tanto, 
 y
y  entonces,
entonces,  y
y  por lo tanto,
por lo tanto, 
Ejercicios.
Evalúe las integrales indefinidas.

INTEGRALES TRIGONOMÉTRICAS
Las integrales trigonométricas implican operaciones algebraicas sobre funciones trigonométricas.
CASO 1.
(i)  o (ii)
o (ii)  donde n es un número entero positivo impar.
donde n es un número entero positivo impar.
 o (ii)
o (ii)  donde n es un número entero positivo impar.
donde n es un número entero positivo impar.
(i) Se hace la transformación

(ii) Se hace la transformación

Leer más: http://www.monografias.com/trabajos68/integrales-indefinidas/integrales-indefinidas2.shtml#ixzz30bxuX8I9